 |
Introduction to point processes |
|
Maximum likelihood estimation for point processes:
Let X be a point process.
A density of X can depend on the positions of the points in a given
realization, or the number of points or the distance between the
points and much more.
Let the density be parametrized by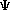 
and denote the density
f(.;).
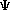Suppose that we have observed a point pattern, say x.
This could be the positions of trees in a forrest.
We want to find the best model for x among f(.;)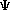
for varying 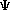, i.e. the model where x is most likely.
This is done (maximum likelihood estimation) by chosing the value of
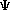that maximizes f(x;).
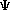This is called the maximum likelihood estimate (MLE).
We find the MLE by solving the equation d/d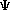
f(.;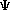) = 0.
This is called the maximum likelihood equation.
Partial (profile) maximum likelihood estimation is when some of the parameters
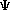( can be higher dimensional) are fixed and the rest are being
estimated.
Partial maximum likelihood estimation
for the Strauss point process:
For a particular class of densities (exponential model), the maximum
likelihood equation becomes E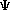 t(X) = t(x),
where t(x) is a vector of
statistics and E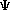 denote the mean.
Two points are said to be R-neighbours if they lie closer than R>0.
For the Strauss process,
=(
,
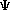,R)
and t(x)=(n(x),s(x;R)), where n(x) is the number of
points in the point pattern x and s(x;R) is the number of R-neighbours in
x.
The Strauss process is an exponential model if R is fixed.
Thus, the partial (R fixed) maximum likelihood equations for the Strauss
process are
E,,
n(X) = n(x) and
E,, s(X;R) = s(x;R).
In order to calculate the full MLE, the partial MLE
((R),(R)) is computed
for each value of R in a grid. Then the values of the partially maximized
likelihood function is computed (up to a constant) for each R, and maximized
in order to find the MLE of R and the corresponding MLE of
(,).
Simulation and approximation:
The density can be written as
f(x;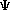)=h(x;)/
(),
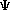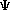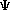where h(x;) is explicitely described, and
()=
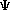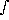
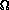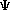h(x;)dx
is intractable and referred to as the normalizing constant.
Therefore the density cannot be calculated explicitely.
Markov chain Monte Carlo methods can be used to simulate a realization drawn
from a given distribution. Let
x1,...,xm
be realizations from the distribution with parameters
(,,R).
Then the mean value is approximated by the sample mean,
E,,
n(X)  |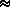
1 |
/ |
m |
 |
|
n(x |
|
) |
and |
E,,
s(X;R) |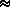
1 |
/ |
m |
|
|
s(x |
|
;R) |
It is not possible to compute the density, but using importance sampling
(combined with bridge sampling) the density can be approximated up to
a constant. No further details will be given here.
|
This page was last modified on September 28th 2001 |
