arallel
programming and Visualization project:
|
Project description
Goal:
We will make a table
(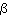 ,
,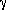 ,R) ->
(E
,R) ->
(E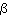 ,
,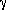 ,
, n(X),
E
n(X),
E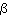 ,
,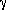 ,
, s(X;R)), such that given a point pattern and an R, the MLE can be found
quickly by the inverse mapping.
s(X;R)), such that given a point pattern and an R, the MLE can be found
quickly by the inverse mapping.
Notice, that not knowing the value of R, we get a whole set of
MLE's, one for each value of R,
{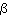 (R),
(R),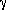 (R),R):R> 0}.
(R),R):R> 0}.
Parallelisation:
There are three levels of iterations:
- (3) Tabulate (E
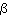 ,
,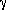 ,
, n(X),E
n(X),E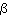 ,
,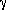 ,
, s(X;R)) for a fine grid of
(
s(X;R)) for a fine grid of
(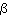 ,
,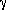 ,R)
,R)
- (2) For each grid value, m realizations from the Strauss model
is drawn (to approximate the means)
- (1) To draw one realization we have to run n_burn steps in a MCMC
algorithm
| (1): |
It does not make sense to parallelize the n_burn
steps of the MCMC
algorithm since these steps are very dependent on each other and
use all the available information. |
| (2): |
The m realizations have to be independent of each
other and therefore it would be evident to parallelize this
step. However, for MCMC algorithms, the time consuming part is for the
chain to reach equilibrium (after the n_burn steps).
Once equilibrium has been reached, the chain can be run
a little longer n_spac
and draw a new realization which of course is dependent of the first
drawn realization, but not very much. |
| (3): |
The operations between grid values are totally
independent
since the parameters of the model are changed. So this part can with
great advantage be made (embarrassing) parallel. |
We have to take into account that the actual value of
(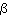 ,
,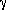 ,R)
have a large impact on the run-time, since a larger
,R)
have a large impact on the run-time, since a larger
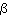 value gives a higher number of points in the realizations and
therefore each step of the Markov chain will take longer time.
value gives a higher number of points in the realizations and
therefore each step of the Markov chain will take longer time.
Therefore the CPU's have to work independently of each other,
and we have to reserve one CPU to keep track of which grid values
that has been calculated and tell the other CPU's which is
the next non-treated grid value. Alternatively we can try to split the
grid up in portions of similar time consumption, but this might be very
difficult, in particular because we work with randomness.
First thing to do is to find the actual run-time for different grid values.
Visualisation:
For fixed R the surfaces
(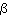 ,
,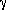 ) ->
E
) ->
E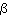 ,
,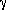 ,
, n(X)
and
(
n(X)
and
(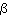 ,
,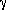 ) ->
E
) ->
E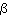 ,
,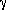 ,
, s(X;R)
are computed in some grid values. The surfaces are
smoothed and approximated using standard statistical techniques and
plotted. A new picture is created for each R, and an
animation can be made with R as the time. The actual values of n(x) and
s(x;r) are plotted as intersecting planes. If the visualisation can be done
while simulating, then the algorithm can be adapted to the output.
We expect the surfaces to be smooth and have controlled behaviour,
so the grid points can be chosen to lie around the grid values producing
mean values close to the actual values.
s(X;R)
are computed in some grid values. The surfaces are
smoothed and approximated using standard statistical techniques and
plotted. A new picture is created for each R, and an
animation can be made with R as the time. The actual values of n(x) and
s(x;r) are plotted as intersecting planes. If the visualisation can be done
while simulating, then the algorithm can be adapted to the output.
We expect the surfaces to be smooth and have controlled behaviour,
so the grid points can be chosen to lie around the grid values producing
mean values close to the actual values.
|
This page was last modified on September 28th 2001 |

